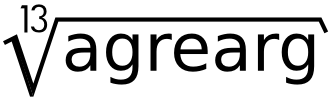
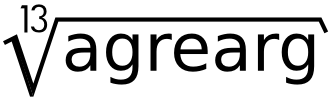Vagrearg Logo  
 

gcmc - G-Code Meta Compiler

Library functions

canned_drill.inc.gcmc

undef canned_drill ( vectorlist:holelist, scalar:retractz, scalar:dw, scalar:oldz )
holelist vectorlist [distance] Vectors pointing to the holes to drill
retractz scalar [distance] Z-axis retract level (R-plane)
dw scalar [none] Dwell time at bottom of hole if ≥0. No dwell is performed if <0
oldz scalar [none] Boolean to indicate if retract should return to original Z
Perform a canned drilling cycle with optional dwelling at the bottom of the hole. The position of the holes are set by the holelist argument where holelist[0] must include a Z-coordinate to set the drilling depth. Each vector in holelist may include X-, Y- or both XY-coordinates to set the position of each drill-hole. An optional Z-coordinate for each vector in holelist may set a new drilling depth for the following hole(s).

The retractz argument sets the R-plane. The R-plane defines the Z-level at which further down-movement is performed at the current feedrate. The actual retraction point depends on oldz, where true means full retraction to the Z-level before the canned_drill() function was called. Setting oldz to false retracts to the R-plane after each drilling sequence. The retractz level is used instead of the original Z-level if the original Z-level was below the R-plane.

The canned_drill() function calls pathmode(1) to set exact path mode before attempting any movement.
undef canned_drill_peck ( vectorlist:holelist, scalar:retractz, scalar:incr, scalar:oldz )
holelist vectorlist [distance] Vectors pointing to the holes to drill
retractz scalar [distance] Z-axis retract level (R-plane)
incr scalar [distance] Incremental drilling depth; must be >0
oldz scalar [none] Boolean to indicate if retract should return to original Z
Perform a canned peck-drilling cycle with incr denoting the incremental down-move distance before clearing the hole. The position of the holes are set by the holelist argument where holelist[0] must include a Z-coordinate to set the drilling depth. Each vector in holelist may include X-, Y- or both XY-coordinates to set the position of each drill-hole. An optional Z-coordinate for each vector in holelist may set a new drilling depth for the following hole(s).

The retractz argument sets the R-plane. The R-plane defines the Z-level to reach to clear the hole. The final retraction point depends on oldz, where true means full retraction to the Z-level before the canned_drill_peck() function was called. Setting oldz to false retracts to the R-plane after each drilling sequence. The retractz level is used instead of the original Z-level if the original Z-level was below the R-plane.

The canned_drill_peck() function calls pathmode(1) to set exact path mode before attempting any movement.

Canned drilling examples

See also the distribution's example file example/canned.gcmc. 
include("canned_drill.inc.gcmc");

homepos = [0mm, 0mm, 0mm];
initpos = [-1mm, -1mm, 10mm];	/* Somewhere to start */

retract = 5.0mm;		/* R-plane level */
incr = 2.2mm;			/* Peck increment */

feedrate(100.0mm);

goto(homepos);
move(homepos);	/* Just to let LinuxCNC show a line in the preview */

/* A set of holes */
holes = {
	[10mm, 0mm, -5mm],	/* First hole at 10,0 depth -1 */
	[15mm],			/* Second hole at X=15 same Y and depth */
	[20mm],
	[25mm],
	[-, 5mm],		/* Move only in Y */
	[20mm],
	[15mm, -, -6mm],	/* Set new drilling depth */
	[10mm]
};

goto(initpos);
canned_drill(holes, retract, -1, 0);	/* Drill a set of holes */

/* Set a new set of holes with explicit coordinates */
holes = {
	[10mm, 20mm, -5mm],
	[15mm, 20mm],
	[20mm, 20mm],
	[25mm, 20mm],
	[25mm, 25mm],	
	[20mm, 25mm],
	[15mm, 25mm, -6mm],
	[10mm, 25mm]
};

goto(initpos + [-, 20]);
canned_drill_peck(holes, retract, incr, 1);	/* Peck-drilling */

goto(head(homepos, 2));
goto(homepos);

tracepath.inc.gcmc

undef tracepath ( vectorlist:path, scalar:z = undef(), scalar:dw = -1 )
path vectorlist [distance] Vectors pointing to the XY positions to visit
z scalar [distance] Cutting plane Z-level
dw scalar [none] Dwell time at bottom each point if ≥0. No dwell is performed if <0
Cut a path at depth z following all points as defined by path. The tracepath() function performs a preliminary movement to path[0] at the current Z-level, moves to cutting depth according to the z argument, visits each vector of path and finally retracts to original Z-level. Movement in the Z-axis can be suppressed by setting the z argument to undef(), which is the default if not specified.

A dwell of length dw is performed at each point in the path if it is ≥0. Any negative value of dw will suppress dwelling. No dwelling is performed if the argument is not supplied.

Tracepath example

include("tracepath.inc.gcmc");

starpath = {
	[ 1,  1], [ 0,  3],
	[-1,  1], [-3,  0],
	[-1, -1], [ 0, -3],
	[ 1, -1], [ 3,  0]
};

SAFEZ = [0mm, 0mm, 1mm];

feedrate(100.0mm);
goto(SAFEZ);

starpath *= 10mm;	/* Scale the star */

tracepath(starpath, -1mm, -1);

goto(SAFEZ);

tracepath_comp.inc.gcmc

undef tracepath_comp ( vectorlist:path, scalar:width, scalar:flags )
path vectorlist [distance] Vectors pointing to the XY positions to visit.
width scalar [distance] Compensation distance
flags scalar [none] Binary flags or'ed together to set the operational mode:
TPC_CLOSEDInterpret path as being closed (path[0] and path[-1] are connected)
TPC_KEEPZDon't move on Z-axis and ignore all Z-coordinates of the path
TPC_OLDZReturn to Z-coordinate where it was before calling the function
TPC_LEFTTrace at left side of path
TPC_RIGHTTrace at right side of path (default)
TPC_ARCINArc in-to the path
TPC_ARCOUTArc out-of the path
TPC_QUIETDon't warn on unreachable inside corners
Cut the path at a tool-compensated distance of width at the left or right side of the path. The right side, set by flag TPC_RIGHT, is seen as being right from a path that moves in positive Y-direction. The left side, set by flag TPC_LEFT, is consequently on the left from a path moving in positive Y-direction.

The cutting depth is set by the Z-coordinate of the first entry at path[0]. Subsequent path entries may contain same or different Z-coordinates. All Z-coordinates will be ignored when flag TPC_KEEPZ is set and no Z-axis movement is performed. The Z-coordinate at function-entry will be restored with a rapid when the TPC_OLDZ flag is set

Entry and exit of the path is controlled by the TPC_ARCIN and TPC_ARCOUT flags. The path is entered with a 90 degree arc to the normal at the first point and exited with a 90 degree arc from the normal at the last point respectively. The arc's radius is equal to width. If the flag is unset, then a linear, perpendicular to the segment, move is performed of length width.

Internal corners which are too small to enter will be deleted from the path and a warning is issued, unless the TPC_QUIET is set. Entering and exiting a closed path on a corner of <180 degrees will result in a warning because the entry and exit positions will cause an inward cut less than width. Co-linear segments are combined into a single segment. A warning is emitted if a Z-axis change is detected on to points with equal X- and Y-coordinates.

Note: Only one point look-ahead is performed on calculations and segments. Therefore, unreachable internal pockets and angles are not detected if hidden beyond one point look-ahead. You should always check the result before accepting it.

Tool-compensated trace example

include("tracepath_comp.inc.gcmc");

starpath = {
	[ 0,  3], [-1,  1],
	[-3,  0], [-1, -1],
	[ 0, -3], [ 1, -1],
	[ 3,  0], [ 1,  1]
};

HOME = [0.0mm, 0.0mm, 1.0mm];

feedrate(100.0mm);
goto(HOME);
move(HOME);			// To visualize following rapids

starpath *= 10.0mm;		// Scale the star

// Show original path as rapids
foreach(starpath; v) {
	goto(v);
}

starpath[0][2] = -1.0mm;	// Set the cutting depth
tracepath_comp(starpath, 2.0mm, TPC_OLDZ|TPC_RIGHT|TPC_ARCIN|TPC_ARCOUT|TPC_CLOSED);

goto(HOME);

engrave.inc.gcmc

undef engrave ( vectorlist:strokes, scalar:zup, scalar:zdown )
strokes vectorlist [distance] Vectors pointing to the XY positions to visit
zup scalar [distance] Pen-up level, i.e. non-engraving-plane/safe Z-level
zdown scalar [distance] Pen-down level, i.e. engraving-plane Z-level
Engrave/cut a path at depth zdown following all points as defined by strokes. The points in the path usually come from the typeset() function after scaling and positioning the XY coordinates. The Z-coordinate holds the instructions for pen-up/down movements.

The strokes argument must include separate vectors which have only a Z-coordinate. A Z-coordinate value of 0.0 means pen-down. Any value >0.0 means pen-up. A pen-down instruction will execute a move([-, -, zdown]) and a pen-up instruction will execute a goto([-, -, zup]).

All other vectors in the strokes argument should have both X and Y coordinates set. A move() is executed for each vector from the list while the pen is downand a goto() for each vector while the pen is up.

The construction of the strokes argument should have the following format (which typeset() follows): 
veclist[0]   = [-, -, 1.0];			/* Pen-up */
veclist[1]   = [x0, y0, -];			/* Left-bottom corner of text */
/* Strokes of the glyphs follow */
veclist[2]   = [x, y, -];			/* Entry point for first stroke */
veclist[3]   = [-, -, 0.0];			/* Pen-down */
... lots of entries up to n-2 ...
veclist[n-1] = [-, -, 1.0];			/* Pen-up */
veclist[n]   = [end_x_pos, end_y_pos, -];	/* Final position would be start of next glyph */

Text engraving example

include("engrave.inc.gcmc");

feedrate(100.0mm);

text = "Hello World! All your Glyphs are belong to us.";
sf = 2.5mm;	/* Scaling factor for 2.5mm height characters */

/*
 * Engrave a scaled version of a typeset text.
 *
 * The height of the returned typeset text is by definition 1.0. The height is
 * relative to the upper case letter 'X' of the font-face. The line-offset is
 * usually in the order of two times the font-height.
 */

/* Typeset the text */
vl = typeset(text, FONT_HSANS_1);

/* Scale XY to real world coordinates */
/* Do not touch the Z-coordinate, the engrave() function needs the original */
vl = scale(vl, [sf, sf]);

/* Place somewhere in XY space */
/* Again without touching the Z-coordinate */
vl += [10.0mm, 18.0mm];

/* Engrave it (output move/goto) with pen-up at 1.5mm and pen-down at -1.0mm */
engrave(vl, 1.5mm, -1.0mm);

varcs.inc.gcmc

Vectorized arcs and circles always return a vectorlist calculated from the origin [0.0, 0.0] or [0.0, 0.0, 0.0] of the coordinate system. The origin point is not included in the vectorlist. The vectorlist is calculated in 2D when two coordinates are provided in the endpoint/centerpoint arguments and calculated in 3D when three coordinates are provided. The 2D coordinates that must be supplied depend on the plane of calculation, actplane, which defaults to the XY plane.

The arc/circle is traced at discrete points at intervals not larger than specified to the function. Two constants are used as defaults for maximum intervals: 
const VARCS_DEFAULT_MAXL = 0.1mm;
const VARCS_DEFAULT_MAXA = 1.0deg;
The distance between calculated points is the same for each point. Arcs and circles with large radii will normally be limited by the maxl argument, whereas small radii will normally hit the maxa limit.

vectorlist varc_cw ( vector:endpoint, scalar:radius, scalar:turns = 0, scalar:maxl = VARCS_DEFAULT_MAXL, scalar:maxa = VARCS_DEFAULT_MAXA, scalar:actplane = PLANE_XY )
vectorlist varc_ccw ( vector:endpoint, scalar:radius, scalar:turns = 0, scalar:maxl = VARCS_DEFAULT_MAXL, scalar:maxa = VARCS_DEFAULT_MAXA, scalar:actplane = PLANE_XY )
endpoint vector [distance] Vector pointing to the endpoint of the arc
radius scalar [distance] The radius of the arc. Positive value indicates shortest angular path, negative value indicates longest angular path
turns scalar [none] Additional full circular turns before ending at endpoint
maxl scalar [distance] Maximum arc segment distance step size
maxa scalar [angle] Maximum arc segment angular step size
actplane scalar [none] Plane of operation, one of PLANE_XY, PLANE_XZ or PLANE_YZ
The varc_cw() and varc_cw() functions return a vectorlist with the vectors to each equally distanced intermediate point in clockwise and counter-clockwise orientation respectively. The arc is calculated from the origin to the endpoint with size of radius. The origin is not included in the returned vectorlist.

The arc is interpolated between the points determined by actual distance or angular movement with a maximum of maxl or maxa. The argument resulting in most interpolated points is used for the calculation.

The arc is calculated in 2D if only two coordinates are present in the endpoint. An optional non-zero third coordinate for 3D operation will create a spiral.

The turns argument indicates the number of full (circular) turns to perform before the final arc is created.
vectorlist vcircle_cw ( vector:centerpoint, scalar:turns = 0, scalar:maxl = VARCS_DEFAULT_MAXL, scalar:maxa = VARCS_DEFAULT_MAXA, scalar:actplane = PLANE_XY )
vectorlist vcircle_ccw ( vector:centerpoint, scalar:turns = 0, scalar:maxl = VARCS_DEFAULT_MAXL, scalar:maxa = VARCS_DEFAULT_MAXA, scalar:actplane = PLANE_XY )
centerpoint vector [distance] Vector pointing to the center of the circle
turns scalar [none] Additional full circular turns before ending back at the origin
maxl scalar [distance] Maximum arc segment distance step size
maxa scalar [angle] Maximum arc segment angular step size
actplane scalar [none] Plane of operation, one of PLANE_XY, PLANE_XZ or PLANE_YZ
The vcircle_cw() and vcircle_cw() functions return a vectorlist with the vectors to each equally distanced intermediate point in clockwise and counter-clockwise orientation respectively. The circle is calculated from the origin and all the way back with the center located at centerpoint. The origin is not included as a start point in the returned vectorlist, but the last point in the vectorlist is the origin (possibly offset in the third coordinate).

The circle is interpolated between the points determined by actual distance or angular movement with a maximum of maxl or maxa. The argument resulting in most interpolated points is used for the calculation.

The circle is calculated in 2D if only two coordinates are present in the centerpoint. An optional non-zero third coordinate for 3D operation will create a spiral.

The turns argument indicates the number of full (circular) turns to perform before the final circle is created.

Vectorized arcs example

include("varcs.inc.gcmc");

radius = 25.0mm;
center = [60.0mm, 100.0mm];
zmove  = 20.0mm;
turns  = 5;

cp = normalize(center) * radius;	// Center point for calculation. The center point
					// also sets the entry angle for the circle.
cp.z = zmove;				// And put in the z-movement

// Get the basic shape
spiral = vcircle_cw(cp, turns);

// The origin point in 'spiral' is [0, 0, 0] by definition
// but it has not been included in the vectorlist

// Offset the spiral to the correct location in space
spiral += center - head(cp, 2);

feedrate(300.0mm);

// Goto the starting point og the spiral
goto(head(spiral[-1], 2));	// Only in XY
goto([-, -, 0.0mm]);		// Reposition in Z

// And cut to each point
foreach(spiral; v) {
	move(v);
}

goto([0.0mm, 0.0mm]);
goto([-, -, 0.0mm]);

vbezier.inc.gcmc

Calculate the vectorization of quadratic or cubic Bezier curves. The functions return a vectorlist with the interpolated points. The points are not spaced equally, but calculated to a certain accuracy using the flatness and minl arguments as limits.

The accuracy arguments have defaults as set by the following constants: 
const VBEZIER_DEFAULT_FLATNESS = 1.0e-4;
const VBEZIER_DEFAULT_MINL = 0.1mm;
The returned vectorlist does not include the (left-side) starting point b0. However, the (right-side) end-point is included as the last point in the list.

Note: the left- and right-side terminology refers to the sequence of arguments, not the position in space.

vectorlist vbezier2 ( vector:b0, vector:b1, vector:b2, scalar:flatness = VBEZIER_DEFAULT_FLATNESS, scalar:minl = VBEZIER_DEFAULT_MINL )
b0 vector [distance] Left-side node of the curve
b1 vector [distance] Control point
b2 vector [distance] Right-side node of the curve
flatness scalar [none] Residual curve angle in interpolation (0 < flatness < 2.0).
minl scalar [distance] Minimum distance between points in the interpolation, must be larger than zero
Returns the vectorization of a quadratic Bezier curve defined by points b0, b1 and b2. The quadratic form is internally converted into a cubic form and calls vbezier3() for the actual calculation. See vbezier3() for details.
vectorlist vbezier3 ( vector:b0, vector:b1, vector:b2, vector:b3, scalar:flatness = VBEZIER_DEFAULT_FLATNESS, scalar:minl = VBEZIER_DEFAULT_MINL )
b0 vector [distance] Left-side node of the curve
b1 vector [distance] Left-side control point
b2 vector [distance] Right-side control point
b3 vector [distance] Right-side node of the curve
flatness scalar [none] Residual curve angle in interpolation (0 < flatness < 2.0).
minl scalar [distance] Minimum distance between points in the interpolation, must be larger than zero
Returns the vectorization of a cubic Bezier curve defined by points b0, b1, b2 and b3. The returned vectorlist does not include the starting point b0 and includes the end point b3 as last in the list. The interpolation of the curve is calculated using De Casteljau's algorithm.

The intermediate points of the curve are placed according to two criteria. The minl argument sets the smallest allowed distance between the points in the vectorlist. The flatness argument is the sum of the maximum allowed residual angle between a flat inter-connect and the actual curve between the calculated points, as seen from both points towards each other, expressed as the cosines of the angles:
2-|cos(left)+cos(right)| < flatness
The test is only performed when the distance between the points is less than ten times minl to ensure only small deviations. The default settings result in about a 10 µm maximum perpendicular deviation from the curve. Reducing flatness by a factor of ten with same minl would result in an error of about 3 µm, at the cost of more points.

Decreasing flatness below 1.0e-9 results in a warning. The machine accuracy is double precision floating point and errors may accumulate to approximately sqrt(<machine accuracy>). Reducing flatness beyond may cause unstable calculation.

Vectors b0, b1, b2 and b3 may be in 2D (XY) space and in 3D (XYZ) vector space. The algorithm is transparent to the dimension and the returned vectorlist will be of same dimension as the input vectors. The limit is that at least X and Y coordinates must be specified. The caller may use other transformations on the returned vectorlist to place the curve anywhere in space afterwards.

Vectorized Bezier curve example

include("vbezier.inc.gcmc");

lp = [10.0mm, 0.0mm];		// Left node point
rp = [20.0mm, 10.0mm];		// Right node point
cpl = lp + [0.0mm, 10.0mm];	// Control point left
cpr = rp + [5.0mm, -5.0mm];	// Control point left

// Calculate the curve
curve = vbezier3(lp, cpl, cpr, rp);

goto(lp);	// Start at starting point
move(curve);	// Trace to the end
 
 
Overengineering @ request