Vagrearg Logo  
 

gcmc - G-Code Meta Compiler

Introduction

Preface

Gcmc is a script language to describe the path of a CNC machine as a high-level language. The output of a gcmc script is G-code, which in turn is interpreted by the CNC machine. Alternatively, gcmc can generate both SVG and DXF output for other machines or uses.

Gcmc syntax is a mainly procedural language where much of the syntax is borrowed from the C language. However, gcmc makes extensive use of vectors and vector-lists, which are the primary types on which operations are performed. The manipulation of vectors is how paths are described.

Why use gcmc instead of G-code?
G-code is a language dating back to 1950s, where computers were in their infancy. Storage and speed were very expensive. Especially storage, done on punch-cards and punch-tape, was reason enough to compact the language into a very basic descriptive language. The now common extensions, allowing complex calculations in G-code stem from the RS274D specification from 1980.
Even with the standardization of G-code, it has always been a challenge to write a G-code program. Mainly because the syntax and semantics are rather difficult to write and read and depend on the ways of things 50 years ago. The emergence of powerful computers as commodity devices allow for a much higher level description of a specific tool-path and allows for a much more readable program-form.
Gcmc is a program to replace the need for having to write archaic G-code without expressiveness for vector concepts, to a form which uses vectors as a main feature for path descriptions. Gcmc has enough power to write readable programs and enough low-level access to direct the CNC machine in a customized way.

First small steps

To get started with gcmc, you need to get a feeling for the basic outline of the language. Question: How to move your machine from one place to another? Answer: 
move([1, 2, 3]);
The above example performs a move at the current feed-rate to coordinates X=1, Y=2 and Z=3. If you instead want to perform a rapid move, then you write: 
goto([0, 0, 10]);
Which moves the machine to coordinates X=0, Y=0, Z=10 as a rapid move.

Both examples use a vector to describe the position to which the machine should move. A vector is enclosed in square brackets ('[' and ']') and contains a comma-separated list of coordinates. Both move() and goto() functions take a vector as argument to emit the command to move the machine.

Vectors may contain undefined coordinates, which instruct the move() and goto() functions to prevent the corresponding axes to move at all. For example, you may wish to move only the Z-axis to ensure the machine to go to a safe height before any other movement is performed. This can be accomplished using: 
goto([-, -, 10]);	/* Move the Z-axis */
goto([0, 0]);		/* Move XY-axes */
A vector coordinate entered as '-' is an undefined entry. A vector's coordinates are interpreted by many functions as [X, Y, Z, A, B, C, U, V, W] and any coordinate not specified omits that axis in the movement output. Vector coordinates omitted at the end of a vector are implied to be undefined. I.e. [1, 2] is interpreted as [1, 2, -, -, -, -, -, -, -] when movement is concerned.

Comments in the gcmc source are entered with // or /*...*/, for comments to end-of-line and block-comments respectively.

You can test all examples and see the output when you input them into gcmc. A simple way is to save the example to a file and run gcmc. Under the assumption that you save the example code as "example.gcmc" you can type: 
$ gcmc -q example.gcmc
The '-q' option suppresses any other automatically generated code (prologue/epilogue) to set the CNC machine in a default state. The example output will be written to standard output (the console/terminal). The output can be saved to a file using the '-o ofile.ngc' option, which write the output to a file called "ofile.ngc".

Above examples result in following G-code snippets: 
$ gcmc -q example.gcmc
G1 X1.00000000 Y2.00000000 Z3.00000000

$ gcmc -q example.gcmc
G0 X0.00000000 Y0.00000000 Z10.00000000

$ gcmc -q example.gcmc
G0 Z10.00000000
G0 X0.00000000 Y0.00000000

You would want gcmc to produce a full fledged output file for normal operation. You can specify an output file with the '-o' option like: 
$ gcmc -o example.ngc example.gcmc
Above example generates a file called "example.ngc" containing all gcode for the CNC machine. You can find all command-line options in the gcmc manual page or you may use the '-h' option for a brief listing of all options. The manual page is part of the distribution and also available online.

Using a variable

Simple movement with goto() and move() become quite involved very fast. You want to be able to give symbolic names to a location and also need to calculate new positions. Variables are used to do both. A variable is a symbolic name for a value, location or a list of locations. A simple example, extending from above could look like: 
SafeZ   = [-, -, 10];
HomePos = [0, 0];
goto(SafeZ);	/* Retract Z */
goto(HomePos);	/* Back to home-base */
Variable can be used in calculations and simple vector math may create customized paths is simple ways. One way to create a path is to use a vectorlist type. A vector-list is a comma separated collection of vectors enclosed in curly brackets ('{' and '}'). Such list may be manipulated in different ways for the list to represent specific movement. 
SafeZ   = [-, -, 10];
CutZ    = [-, -, -1];
HomePos = [0, 0];
Square  = { [0, 0], [1, 0], [1, 1], [0, 1] };
goto(Square[3]);	/* To last point */
move(CutZ);		/* Goto cutting depth */
move(Square[0]);	/* Cut the square */
move(Square[1]);
move(Square[2]);
move(Square[3]);
goto(SafeZ);		/* Retract */
goto(HomePos);		/* Back to home-base */
Each element in a vector-list can be addressed using an index starting from zero. However, there is no reason to iterate through all entries manually as it can be performed automatically using a foreach construct. Secondly, the square can be scaled and moved to any size and place using simple math. 
SafeZ   = [-, -, 10];
CutZ    = [-, -, -1];
HomePos = [0, 0];
Square  = { [0, 0], [1, 0], [1, 1], [0, 1] };
Offset  = [-2, 5];
Square  = Square * 10 + Offset;	/* Scale and move the square */
feedrate(100);		/* Set feed so it can be visualized by LinuxCNC */
goto(Square[-1]);		/* To last point */
move(CutZ);			/* Goto cutting depth */
foreach(Square; v) {
	move(v);		/* Cut the square */
}
goto(SafeZ);			/* Retract */
goto(HomePos);			/* Back to home-base */
Above example scales the square by a factor 10 and moves all point of the square -2 in X and +5 in Y, resulting in {[-2, 5], [8, 5], [8, 15], [-2, 15]}.

Another small change can be seen in goto(Square[-1]). The index changes from '3' to '-1'. Indices can be both positive and negative. A positive index starts counting from the start, where 0 (zero) is the first entry. A negative index starts at -1, which indicates the last entry, -2 the second last entry, etc.. Using negative indices is a simple way to get to the last entry/entries of a list if the size of the list is unknown beforehand.

The foreach construct takes the list to iterate over as the first parameter and a second parameter denotes the variable name which will receive the individual vectors. The feedrate() function was added to set the feed-rate of the machine (F word in G-code). LinuxCNC reports an error and refuses to visualize a program if no feed-rate is set (or is zero).

Using units and numbers

CNC machines work in a real world where measures are important. The machines are fed by numbers representing units millimeters or inches. Most machines can be instructed to interpret bare numbers as either, which can lead to a lot of work if designs have origins in both metric and imperial units. Using both metric and imperial units can also be prone to inadvertent errors due to manual conversions.

Gcmc supports the use of units as part of the language and will automatically do all conversions. Gcmc can generate output in either metric or imperial units and, if used consistently, will generate the exact same result in terms of absolute size when either is selected.

Units can be attached to any number in gcmc by appending 'mm', 'in', 'deg' or 'rad' to the number, where deg/rad are angular units degrees and radians respectively. One special form is supported for anyone in PCB design, who will probably know the 'mil' (1/1000 of an inch), which is automatically converted into inches. 
metric   = 100mm;
imperial = 5in;
pcbmils  = 400mil;	/* converted to 0.4in */
degrees  = 30deg;
radians  = 3.14159265359rad;
Any number entered can be of integer or floating point type. Any number containing a decimal point or an exponent is a floating point number. Gcmc preserves the type of number as far as possible, meaning that integers stay integer and floating point stay floating point when ever possible. Floating point numbers are generally never converted into integers, but integers may be promoted to floating point numbers. Beware: many real-world positional calculations require floating point precision. It is often a good idea to ensure that coordinates are floating point and have units associated.

Conversions primarily occur when mixed type calculations are performed and when units need to be converted. 
metric   = 100mm;
imperial = 5in;
mi = metric + imperial;	/* mi becomes metric float 227.0mm */
im = imperial + metric;	/* im becomes imperial float 8.93700787402in */

i1 = 10;
i2 = 4;
divi = i1 / i2;		/* divi becomes integer 2 */

fl = 4.0;
divf = i1 / fl;		/* divf becomes float 2.5 */
Numbers with units associated are converted to the unit on the left-hand-side of the calculation. Unit conversion always implies conversion to floating point. If either of the numbers has no units associated, then the one with units will be used and conversion to floating point will occur only if any is floating point to start with. A more detailed description is available at the unit syntax description with all combinations specified.

Revisiting the example from above with proper units attached may look like: 
SafeZ   = [-, -, 10.0mm];
CutZ    = [-, -, -1.0mm];
HomePos = [0.0mm, 0.0mm];
Square  = { [0, 0], [1, 0], [1, 1], [0, 1] };
Offset  = [-2.0mm, 5.0mm];
Square  = Square * 10.0in + Offset;	/* Scale and move the square */
feedrate(100mm);		/* Set feed so it can be visualized by LinuxCNC */
goto(Square[-1]);		/* To last point */
move(CutZ);			/* Goto cutting depth */
foreach(Square; v) {
	move(v);		/* Cut the square */
}
goto(SafeZ);			/* Retract */
goto(HomePos);			/* Back to home-base */
Please note that the definition of the square has no units attached. The square is an abstract form which receives the actual size and position by 10 inch scaling and metric offsetting. Compiling the example with gcmc gives following results: 
$ gcmc -q example.gcmc
F100.00000000
G0 X-2.00000000 Y259.00000000
G1 Z-1.00000000
G1 X-2.00000000 Y5.00000000
G1 X252.00000000 Y5.00000000
G1 X252.00000000 Y259.00000000
G1 X-2.00000000 Y259.00000000
G0 Z10.00000000
G0 X0.00000000 Y0.00000000

$ gcmc -q -i example.gcmc
F3.93700787
G0 X-0.07874016 Y10.19685039
G1 Z-0.03937008
G1 X-0.07874016 Y0.19685039
G1 X9.92125984 Y0.19685039
G1 X9.92125984 Y10.19685039
G1 X-0.07874016 Y10.19685039
G0 Z0.39370079
G0 X0.00000000 Y0.00000000
The first compilation uses metric mode, whereas the second compilation uses imperial mode ('-i' option). The difference is the absolute values of the coordinates, which are converted to the units which the target uses. Gcmc wil normally insert the appropriate G21/G20 instruction in the prologue (if the '-q' option is omitted) to tell the G-code interpreter that the following coordinates are in millimeters or inches respectively.

Both versions, metric and imperial, have the same absolute sizes and will be cut at the same physical speed because units were consistently used. All the numbers were converted automatically to yield the same physical result. Portable gcmc programs should always make use of units in a consistent manner to ensure correct output when either metric or imperial is used.

User functions

Repeating patterns often occur when machining a particular part. It is often desirable to describe the repeating patterns as a function which can be called over and over again. 
SafeZ   = [-, -, 10.0mm];
CutZ    = [-, -, -1.0mm];
HomePos = [0.0mm, 0.0mm];
Square  = { [0, 0], [1, 0], [1, 1], [0, 1] };

function cut_the_path(path, offset)
{
	path += offset;		/* Move the path to the actual position */
	goto(path[-1]);	/* To last point */
	move(CutZ);		/* Goto cutting depth */
	foreach(path; v) {
		move(v);	/* Cut the path */
	}
	goto(SafeZ);		/* Retract */
}

feedrate(100mm);				/* Set feed so it can be visualized by LinuxCNC */
goto(SafeZ);					/* Initial to safe Z retraction point*/
cut_the_path(Square * 1in, [10.0mm, 5.0mm]);	/* First square */
cut_the_path(Square * 2in, [15.0mm, 15.0mm]);	/* Second square */
cut_the_path(Square * 3in, [20.0mm, 25.0mm]);	/* Third square */
cut_the_path(Square * 4in, [25.0mm, 35.0mm]);	/* Fourth square */
cut_the_path(Square * 5in, [30.0mm, 45.0mm]);	/* Fifth square */
goto(HomePos);					/* Back to home-base */
Functions can take as many parameters as required and are most often passed as values (see functions syntax reference for more details). Above example can be further abstracted by using the repeat construct. The path is cut five times with regular intervals, which can be expressed in a mathematical way: 
SafeZ   = [-, -, 10.0mm];
CutZ    = [-, -, -1.0mm];
HomePos = [0.0mm, 0.0mm];
Square  = { [0, 0], [1, 0], [1, 1], [0, 1] };

function cut_the_path(path, offset)
{
	path += offset;		/* Move the path to the actual position */
	goto(path[-1]);	/* To last point */
	move(CutZ);		/* Goto cutting depth */
	foreach(path; v) {
		move(v);	/* Cut the path */
	}
	goto(SafeZ);		/* Retract */
}

feedrate(100mm);		/* Set feed so it can be visualized by LinuxCNC */
goto(SafeZ);			/* Initial to safe Z retraction point*/
repeat(5; i) {
	cut_the_path(Square * (1.0in + i), [10.0mm, 5.0mm] + [5.0mm, 10.0mm] * i);
}
goto(HomePos);			/* Back to home-base */
The repeat construct sets the variable 'i' to the sequence 1, 2, 3, 4, 5 and is used to calculate the scaling factor by addition and the offset by scaled addition. It should be noted that the scaling "1.0in + i" adds inches and a number without units. Gcmc handles such case by defaulting the units to the side with units associated (see unit description for rules).

A real program - Making gears

So far only introductory commands were shown. A real program consists of a bit more than simple movement on a path. Lets make a gear as a more real-world example. Please note, the author is not a specialist in gear-making and the presented end-result is not intended to be 100% correct nor complete. The information how gears are constructed has been gathered from internet resources using a search-engine as best friend. The rest is, as they say, history.

An involute gear is a gear which has a curved tooth-surface. The basic outline of such gear is: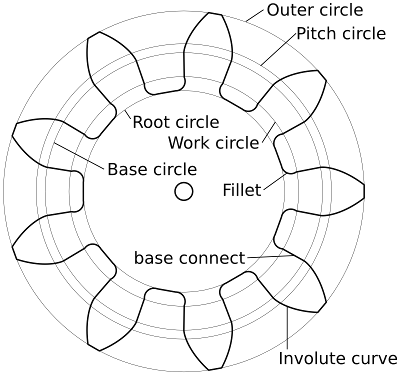
involute-gear-image
The gear has following parameters that need to be input or calculated:
• Pitch circle The circle of tooth contact with another gear
• Outer circle The outer size of the gear
• Work circle The depth of mating gear's tooth
• Root circle Actual depth of the teeth
• Base circle The origin of the involute curve
• Fillet Recessed rounding at bottom of tooth for clearance
• Involute curve Smooth tooth surface for teeth-rollover
• Base connect Connection from the fillet to the involute curve
Additional parameters:
• Number of teeth
• Size of the gear, either by a diameter or by teeth-per-mm (or teeth-per-inch)
• Pressure angle at which the teeth have contact

A gear has a set of parameters and associated names as listed below.
• N Number of Teeth
• Pa Pressure Angle
• D Pitch Diameter D = N/P = Do - 2/P Gear radius at center of the teeth
• P Diametral Pitch P = N/D
• p Circular Pitch p = pi() / P
• Db Base Diameter Db = D * cos(Pa) Bottom of teeth insertion
• Dr Root Diameter Dr = D - 2b Bottom of tooth cutout
• Do Outside Diameter Do = D + 2a
• a Addendum a = 1/P
• b Dedendum b = ht - a
• ht Whole Depth 2.157/P
• hk Working Depth 2*a

It is important to see shortcuts in the design when creating a program. For example, a gear has many symmetries which can be used to reduce the amount of work. Once a small part of the gear is created, it can be duplicated in rotated and mirrored forms quite easily.

The smallest part of the gear that must be calculated is one single side of a tooth. The side of a tooth starts with the fillet and connects to the involute curve. Once this small part is created, it can be duplicated to create a full tooth, which in turn can be duplicated to create the entire gear.

Calculating the basic parameters

The input of the gear-making function will be:
• NNumber of Teeth
• PaPressure Angle
• PDiametral Pitch

All other parameters can be calculated from the above input arguments. The output is a vectorlist containing all points to describe the gear in a 2D path.
function gear_P(nteeth, pressure_angle, diametral_pitch)
{
	local gear = {};
	...
	return gear;
}
There are two new concepts in above function outline. Firstly, the keyword local is used to signal gcmc that the named variable is local to the function being declared. Secondly, the return statements allows the function to return a value back to the caller. The variable "gear" will be containing a list of vectors which are returned to the caller of the function.

The first part of the function consists of calculating the necessary parameters to define the gear from the input arguments. The calculations are as given in above table. The work diameter is given by the working depth, which is twice the addendum. 
function gear_P(nteeth, pressure_angle, diametral_pitch)
{
	local pitch_diameter = nteeth / diametral_pitch;
	local base_diameter = pitch_diameter * cos(pressure_angle);
	local addendum = 1.0/diametral_pitch;
	local ht = 2.157 / diametral_pitch;
	local dedendum = ht - addendum;
	local outside_diameter = pitch_diameter + 2.0*addendum;
	local root_diameter = base_diameter - 2.0*dedendum;
	local work_diameter = outside_diameter - 4.0*addendum;
	...
}
The calculation part of the tooth can start after the parameters are setup. As mentioned above, there are many symmetries and only one side of the tooth needs to be calculated. That part looks like:
involute-gear-tooth-side

Calculating the fillet arc

The first calculation is the radius of the fillet arc. The fillet arc connects to the involute arc through a straight line. The fillet arc should go from the root circle up to the work circle. The known point in the curve is the point on the work circle.

Instead of doing extensive math here, it is enough to estimate the radius of the fillet arc. It turns out that the radius may be approximated by 1/8 of the distance from base to root circles. This measure will create an arc that does not drop onto the root circle exactly. The local variable "filletrad" is set to the appropriate value. Making an exact calculation is left to the reader.
local filletrad = (base_diameter - root_diameter)/8.0;

The fillet arc has an angled connection to the straight line at the work circle. That angle is set at 240 degrees (seen CW). The center of the arc is known to be on a line bisecting that angle and has a length of "filletrad" from the intersection at the work circle.

The vector [-filletrad, 0.0mm] points left and must be rotated 60 degrees CCW to have the same direction as the bisecting line that is sought after. Rotating a vector is performed by: 
rotate_xy([-filletrad, 0.0mm], 60.0deg);
The built-in function rotate_xy() rotates any vector or vectorlist by the angle given. It should be noted that rotate_xy([filletrad, 0.0mm], 240.0deg) would have performed the same function as the minus sign on the X-coordinate equals 180 degree rotation for a vector with zero Y-coordinate.

The center of the fillet arc can now be calculated by adding the distance from the origin to the work circle. The result is a point denoting the center of the fillet arc: 
local center = rotate_xy([-filletrad, 0.0mm], 60.0deg) + [work_diameter/2.0, 0];

The fillet arc could be created with an arc command, but that would not be useful. There is no method to embed non-linear segments in a vector list. A vector-list is a set of points, which will be connected with straight lines. Therefore, the arc must be synthesized with small linear segments. Calculating linear segments is not hard. Points are calculated on the arc at regular angular intervals from start to end. Each calculated point is then added to the result.

It is known that the arc starts at 180 degrees, the vertical tangent, and ends at 60 degrees (i.e. covers 120 degree span). Also, the center point and radius are known. A simple loop can be constructed to calculate points on the arc in following way: 
local i;
local tooth = {};
for(i = 180.0deg; i > 60.0deg; i -= __ang_step*2.5) {
	tooth += { [cos(i), sin(i)] * filletrad + center };
}
if(i != 60.0deg) {
	// Add the last point if we did not reach the working depth
	tooth += { [cos(60.0deg), sin(60.0deg)] * filletrad + center };
}
The first part loops the variable "i" from 180 degrees down to 60 degrees in discrete steps using a for() construct. The decrement for "i" is set at a constant ("__ang_step"), defined somewhere else in the program and default set to 2.0 degrees. The angular step is increased by a factor of 2.5 because small arcs have little movement at small angular intervals. There is no need to be nanometer precise.

The second part has an if() construct to test if the end-point of the arc was exactly reached. If the last angle calculation of "i" was not at 60 degrees, then the next segment, connecting to the involute curve, would be off. Therefore a test is performed and a finalizing point added if necessary.

The calculation of the points on the arc consists of a simple vector geometry, where a unity-circle vector is calculated with sin/cos, scaled to the fillet radius and spatially moved to the correct location. The calculated vector is encapsulated into a new vector list (using '{' ... '}') in order to concatenate vector-lists easily with the '+=' operator.

The end result of the fillet arc calculation as part of the function: 
	...
	local i;
	local tooth = {};

	// Fillet radius is approx. Will not reach root exactly, but close enough
	// Otherwise need to calculate intersection with root-circle
	local filletrad = (base_diameter - root_diameter)/8.0;

	// Center of the fillet arc, involute makes a ~240deg angle with fillet arc
	// The fillet arc runs from the root to the working depth of the gear
	local center = rotate_xy([-filletrad, 0.0mm], 60.0deg) + [work_diameter/2.0, 0];

	// Trace the fillet arc from ~root-circle to working depth at involute arc starting Y-level
	for(i = 180.0deg; i > 60.0deg; i -= __ang_step*2.5) {
		tooth += { [cos(i), sin(i)] * filletrad + center };
	}
	if(i != 60.0deg) {
		// Add the last point if we did not reach the working depth
		tooth += { [cos(60.0deg), sin(60.0deg)] * filletrad + center };
	}
	...

Calculating the involute arc

Next up is the involute arc. The connection between the fillet arc and the involute arc is inherent to the concatenation of points of the tooth's side. The first point of the involute arc is automatically connected with a straight segment to the last point of the fillet arc.

An involute arc is calculated using a radius and an angle. See the Wikipedia article on the subject for detailed formula. There are two formula, the Cartesian and the Polar method. The Cartesian form can be used to create line-segments to define the arc. The Polar form, when rewritten, can be used to determine the maximum arc angle to reach the outer circle.

The involute arc's intersection with the outer circle, in radians, is defined by sqrt((O/B)^2-1), with O outer radius and B base radius of appropriate circles. In gcmc terms: 
function involute_angle(radius, outrad)
{
	return to_rad(sqrt(pow(outrad/radius, 2.0) - 1));
}
The extra to_rad() function is to return a value with radians as units. The sqrt() returns a dimension-less value, but the formula is known to result in a value of radians.

Calculating the points on the involute arc is just as easy. The calculation has both an X- and Y-coordinate, which form a vector, based on the base radius and the angle. Both are combined and return as a point on the arc. The involute_point() function uses to_rad() to ensure that the "angle" argument is in radians, which is required for the formula to function properly.

The to_none() function is used to strip the units within the basic curve calculation. The involute curve describing vector should be dimensionless so it may be scaled to distance units. The conversion to distance units is implied by the multiplication of the "radius" argument, which will be the contributor to the units of the return value. 
function involute_point(angle, radius)
{
	angle = to_rad(angle);	/* Multiplication must be in radians */
	return radius * [cos(angle) + to_none(angle) * sin(angle), sin(angle) - to_none(angle) * cos(angle)];
}
The involute arc is calculated by repeatedly calling the involute_point() function from angles 0 degrees to the maximum angle as returned by function involute_angle() at the outer circle radius. The points are added to the tooth-side under construction just like the fillet arc above. 
	...
	// Calculate the maximum involute angle to intersect at the outside radius
	local max_a = involute_angle(base_diameter/2.0, outside_diameter/2.0);

	// Trace the involute arc from the base up to outside radius
	for(i = 0.0deg; i < max_a; i += __ang_step) {
		tooth += { involute_point(i, base_diameter/2.0)};
	}
	if(i != max_a) {
		// Add the last point if we did not reach the outside radius
		tooth += { involute_point(max_a, base_diameter/2.0)};
	}
	...
The for() loop makes use of gcmc's units and automatic conversions. The loop-variable "i" is specified in degrees, while the "max_a" variable is in radians. The for()-loop condition compares degrees with radians. Gcmc is able to perform correct angular comparison because units are specified on both "i" and "a_max".

Making a tooth, teeth and gear

The program up to now has created a single side of one tooth. The next step is to combine two sides into one whole tooth. The "tooth" variable, used to collect the points of the tooth-side, is oriented in positive X direction and is along the X-axis. If the first complete tooth is considered to be symmetrical at the positive X-axis, then the side must be rotated by "360 divided by four times the number of teeth" degrees. The "four times" stems from a complete tooth comprising of both a high- and low-side, resulting in two half-tooth-pitch sizes of two side each. 
	...
	// We now have one side of the tooth. Rotate to be at tooth-symmetry on X-axis
	tooth = rotate_xy(tooth, -90.0deg / nteeth);
	...
The above snippet will rotate the tooth-side CW by the correct angle.

To complete one tooth, the current side must be mirrored over the X-axis. A mirror over X is the same as a scaling factor of -1 in Y and +1 in X direction. Combining the original and mirrored points requires the mirrored version to have all points reversed because the points need to flow in one direction. 
	...
	// Add the same curve mirrored to make the other side of the tooth
	// Coordinates reverse to have them all in one direction only
	tooth += reverse(scale(tooth, [1, -1]));
	...
The scale() function scales each vector of "tooth" to produce a mirror-over-X copy and the reverse() functions reverses all points from the scaled/mirrored version. The resulting vector-list is concatenated with the original side to produce exactly one full tooth.

The last part to make the gear outline complete is to copy the tooth as many times as there are teeth while rotating it as we go. The result is accumulated in the gear variable and returned from the function. 
	...
	// Create all teeth of the gear by adding each tooth at correct angle
	local gear = {};
	repeat(nteeth; i) {
		gear += rotate_xy(tooth, 360.0deg * i / nteeth);
	}
	return gear;

Finishing touches to make it work

The function gear_P() has now been fully developed and it returns a vector-list with all points of the outline. The outline needs to be output using a simple trace() routine that will do just that. A second small function hole() is created to make the center-hole of the gear. Finally calling it all with some parameters will give a nice set of gears. 
/* Trace a path at given offset */
function trace(path, offset)
{
	goto(path[-1] + offset);
	foreach(path; v) {
		move(v + offset);
	}
}

/* Make a hole at center point with given radius */
function hole(point, radius)
{
	goto(point - [radius]);
	circle_cw_r([radius, 0]);
}

/* -------------------- Main Program -------------------- */

HD = 6.0mm;	// Gear center-hole diameter
N = 9;		// Number of teeth
PA = 20.0deg;	// Pressure angle
D = 100.0mm;	// Pitch diameter
P = N/D;	// Diametral pitch

// First gear
hole([D/2.0, 0.0mm], HD/2.0);
trace(gear_P(N, PA, P), [D/2.0, 0.0mm]);

// Second gear
hole([-D/2.0, 0.0mm], HD/2.0);
trace(gear_P(N, PA, P), [-D/2, 0.0mm]);

The source of the gears example is available from the Gitlab gcmc repository as involute-gear.gcmc and involute-gear.inc.gcmc.
 
 
Overengineering @ request